TEMPEST - High-level Planning in Robotics

High-Level Planning in Robotics

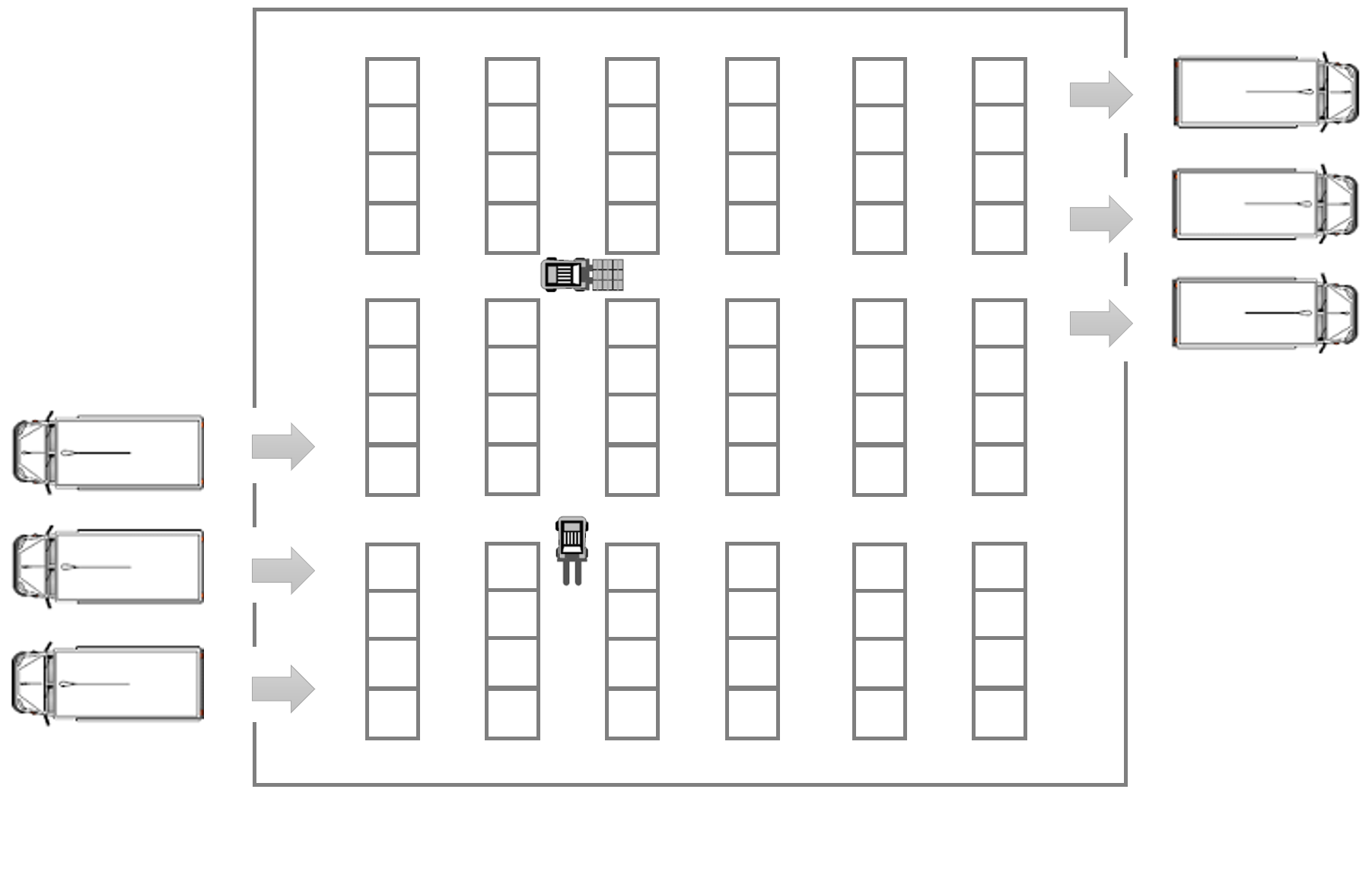
A classical application of reactive synthesis is the domain of automated high-level planning in robotics. We consider a warehouse floor plan with several shelves, see Figure 1. To parametrise the experiment, we consider floor plans with n * 3 shelves with 2 ≤ n ≤ 20. A robot operates together among other robots within the warehouse. TEMPEST can be used in this setting to synthesize controllers for the robot that perform certain tasks, as well as shields used to ensure safe operation of the robot, or to guarantee performance.

The warehouse floor plan as depicted in the paper.

Figure 1: The warehouse floor plan with 6 * 3 shelves.

Controller Synthesis

Using TEMPEST, we synthesize a controller for the robot that repeatedly picks up packages from one of the entrances and delivers them to the exits. We use the mean-payoff criterion to specify that the stochastic shortest paths should be taken. Note, that different specifications for controller synthesis could also be used in TEMPEST.

Model Specification

We discuss the model given in Figure 2 in detail and describe the different sections of the code. The property used to synthesise the optimal controller is given in Figure 3.

The keyword smg defines the model to be a stochastic multiplayer game.

At first we define the actions controllable by each player with the player...endplayer struct. Square brackets indicate an action to be controlled by the described player.

We then define the grid dimension using an undefined constant w. Afterwards we define the boundaries for the movement of the two robots as well as the probability of robot 2 getting stuck.

The global variable move models the turn-based character of the coalition game. It is toggled between the two players such that they may move in an alternating fashion.

Following this we define multiple formulas to capture the spatial constraints given through the environment. A robot may not move into a shelf given that it is between two shelves. If the two robots are above, or below, a row of shelves they may also not move into the shelf. Lastly we capture whether the robots are moving in a corridor between the rows of shelves.

Next, we label all states for which the robots are on the same field with crash.

smg

player controlledRobot
  [e1], [w1], [n1], [s1], [pickUp], [deliver]
endplayer

player adverseryRobot
  [e2], [w2], [n2], [s2]
endplayer

// (w+1)x16 - grid
const int w;
const int width = w;
const int height = 15;

const int xmin = 0;
const int xmax = width;
const int ymin = 0;
const int ymax = height;

// probabilty to get stuck
const double stuckProp = 1/5;
const double notstuckProp = 1 - stuckProp;

global move : [0..1] init 0;

formula robot1BetweenShelves = !(y1=0 | y1=height);
formula robot2BetweenShelves = !(y2=0 | y2=height);
formula robot1AboveShelves = mod(x1, 2) = 1;
formula robot1BelowShelves = mod(x1, 2) = 1;
formula robot2AboveShelves = mod(x2, 2) = 1;
formula robot2BelowShelves = mod(x2, 2) = 1;
formula robot1OpenRow = mod(y1, 5) = 0;
formula robot2OpenRow = mod(y2, 5) = 0;

label "crash" = x1=x2 & y1=y2;

module robot1
  x1 : [0..width] init width;
  y1 : [0..height] init 0;
  picked_up : bool init false;

  [e1]    move=0 & x1<xmax & (!robot1BetweenShelves | robot1OpenRow) -> (x1'=x1+1) & (move'=1);
  [w1]    move=0 & x1>0    & (!robot1BetweenShelves | robot1OpenRow) -> (x1'=x1-1) & (move'=1);

  [n1]    move=0 & y1>0    & !robot1BelowShelves -> (y1'=y1-1) & (move'=1);
  [s1]    move=0 & y1<ymax & !robot1AboveShelves -> (y1'=y1+1) & (move'=1);

  [pickUp] move=0 & !picked_up & x1=0 & y1=ymax -> (picked_up'=true) & (move'=1);
  [deliver] move=0 & picked_up & x1=width & y1=0 -> (picked_up'=false) & (move'=1);
endmodule

module robot2
  x2 : [0..width] init xmax;
  y2 : [0..height] init 0;

  [e2]    move=1 & x2<xmax & (!robot2BetweenShelves | robot2OpenRow) -> notstuckProp : (x2'=x2+1) & (move'=0) + stuckProp : (move'=0);
  [w2]    move=1 & x2>0    & (!robot2BetweenShelves | robot2OpenRow) -> notstuckProp : (x2'=x2-1) & (move'=0) + stuckProp : (move'=0);

  [n2]    move=1 & y2>0    & !robot2BelowShelves -> notstuckProp : (y2'=y2-1) & (move'=0) + stuckProp : (move'=0);
  [s2]    move=1 & y2<ymax & !robot2AboveShelves -> notstuckProp : (y2'=y2+1) & (move'=0) + stuckProp : (move'=0);
endmodule

rewards
  true : -1;
  x1=x2 & y1=y2 : -25;
  [deliver] true : 100;
endrewards

Figure 2: PRISM input model file for the optimal controller. [raw]

The main part of the modelling is described by the module structs. Via these we describe the environment and the movement of the robots. robot1 (controlled by player controlledRobot, see above) starts at position (width,0) and has not picked up its package yet.

The actions available to the robots are modelled as such:

[e1]    move=0 & x1<xmax & (!robot1BetweenShelves | robot1OpenRow) -> (x1'=x1+1) & (move'=1);

[e1] is the label of the action.
move=0 & x1<xmax & (!robot1BetweenShelves | robot1OpenRow) is called the guard of the action, describing whether this action is enabled or not.
(x1'=x1+1) & (move'=1); finishes the command by describing the outcome distribution when taking this action.

The robots may move in four directions along the axis, given they current position. robot1 has the additional objective to pick up packages. Whenever it is in the correct position it may either pickUp a package or deliver it at the departure gate.

In order to synthesise an optimal route, given the adversarial behaviour of robot2 we need to define certain negative and positive rewards. Whenever the robots move a negative reward, or cost, of -1 is applied. Crashing costs an additional value of -25. If robot1 manages to pick up and deliver a package it is awarded a value of 100.

The property specification shown below is used to synthesise the optimal controller. It defines the coalition to consist out of the player controlling robot1. We then tell TEMPEST to synthesise a strategy which maximizes the described reward in the long-run average. TEMPEST allows the usage of both the S and LRA operators for the computation of the long-run average.

<<controlledRobot>> Rmax=? [ LRA ];

Figure 3: PRISM property specification for the optimal controller. [raw]

Results

The results for the synthesis times are depicted in Figure 4. The sizes of state space of the game graphs range from 5184 states for n=2 to 186624 states for n=20. The results for optimal-shields use the axis on the right hand-side. To compare our results, we tried to compute a strategy for the optimal controller in PRISM-games 3.0 which resulted in an error. By proper modelling, we were able to synthesize a safe controller comparable to the safety-shield using PRISM-games 3.0, resulting in better synthesis times for TEMPEST.

The plot containing different synthesis times in the robotics setting.

Figure 4: The results of all three experiments for the warehouse setting. Consider the red plot.