High-Level Planning in Robotics

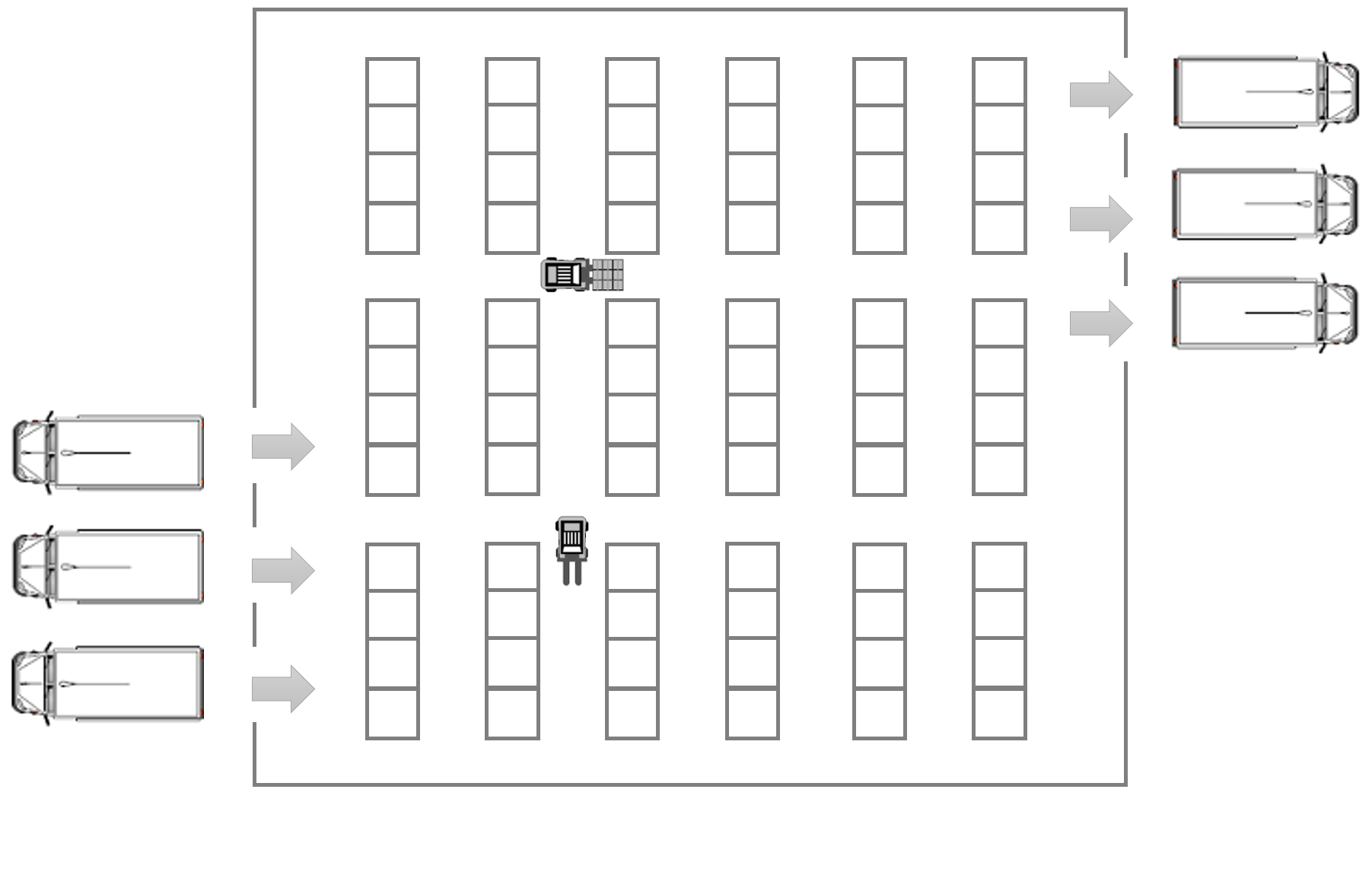
A classical application of reactive synthesis is the domain of automated high-level planning in robotics. We consider a warehouse floor plan with several shelves, see Figure 1. To parametrise the experiment, we consider floor plans with n * 3 shelves with 2 ≤ n ≤ 20. A robot operates together among other robots within the warehouse. TEMPEST can be used in this setting to synthesize controllers for the robot that perform certain tasks, as well as shields used to ensure safe operation of the robot, or to guarantee performance.

The warehouse floor plan as depicted in the paper.
Figure 1: The warehouse floor plan with 6 * 3 shelves.

Safety-Shield Synthesis

A safety-shield can be synthesized to enforce collision avoidance with other robots. In the experiments, we used a finite horizon of 14 steps and a relative threshold of lambda = 0.9.

Model Specification

We discuss the model given in Figure 2 in detail and describe the different sections of the code. The property used to synthesise the safety shield is given in Figure 3.

The keyword smg defines the model to be a stochastic multiplayer game.

At first we define the actions controllable by each player with the player...endplayer struct. Square brackets indicate an action to be controlled by the described player.

We then define the grid dimension using an undefined constant w. Afterwards we define the boundaries for the movement of the two robots as well as the probability of robot 2 getting stuck.

The global variable move models the turn-based character of the coalition game. It is toggled between the two players such that they may move in an alternating fashion.

Following this we define multiple formulas to capture the spatial constraints given through the environment. A robot may not move into a shelf given that it is between two shelves. If the two robots are above, or below, a row of shelves they may also not move into the shelf. Lastly we capture whether the robots are moving in a corridor between the rows of shelves.

Next, we label all states for which the robots are on the same field with crash. 

smg

player shieldedRobot
  [e1], [w1], [n1], [s1]
endplayer

player adverseryRobot
  [e2], [w2], [n2], [s2]
endplayer

// (w+1)x16 - grid
//const int w;
const int width = 6;
const int height = 15;

const int xmin = 0;
const int xmax = width;
const int ymin = 0;
const int ymax = height;

// probabilty to get stuck
const double stuckProp = 1/5;
const double notstuckProp = 1 - stuckProp;

global move : [0..1] init 0;

formula robot1BetweenShelves = !(y1=0 | y1=height);
formula robot2BetweenShelves = !(y2=0 | y2=height);
formula robot1AboveShelves = mod(x1, 2) = 1;
formula robot1BelowShelves = mod(x1, 2) = 1;
formula robot2AboveShelves = mod(x2, 2) = 1;
formula robot2BelowShelves = mod(x2, 2) = 1;
formula robot1OpenRow = mod(y1, 5) = 0;
formula robot2OpenRow = mod(y2, 5) = 0;

label "crash" = x1=x2 & y1=y2;

module robot1
  x1 : [0..width] init 0;
  y1 : [0..height] init ymax;

  [e1]    move=0 & x1<xmax & (!robot1BetweenShelves | robot1OpenRow) -> (x1'=x1+1) & (move'=1);
  [w1]    move=0 & x1>0    & (!robot1BetweenShelves | robot1OpenRow) -> (x1'=x1-1) & (move'=1);

  [n1]    move=0 & y1>0    & !robot1BelowShelves -> (y1'=y1-1) & (move'=1);
  [s1]    move=0 & y1<ymax & !robot1AboveShelves -> (y1'=y1+1) & (move'=1);
endmodule

module robot2
  x2 : [0..width] init xmax;
  y2 : [0..height] init 0;

  [e2]    move=1 & x2<xmax & (!robot2BetweenShelves | robot2OpenRow) -> notstuckProp : (x2'=x2+1) & (move'=0) + stuckProp : (move'=0);
  [w2]    move=1 & x2>0    & (!robot2BetweenShelves | robot2OpenRow) -> notstuckProp : (x2'=x2-1) & (move'=0) + stuckProp : (move'=0);

  [n2]    move=1 & y2>0    & !robot2BelowShelves -> notstuckProp : (y2'=y2-1) & (move'=0) + stuckProp : (move'=0);
  [s2]    move=1 & y2<ymax & !robot2AboveShelves -> notstuckProp : (y2'=y2+1) & (move'=0) + stuckProp : (move'=0);
endmodule
Figure 2: PRISM input model file for synthesis of the safety shield. [raw]

The main part of the modelling is described by the module structs. Via these we describe the environment and the movement of the robots. robot1 (controlled by player controlledRobot, see above) starts at position (0,ymax).

The actions available to the robots are modelled as such: 

[e1]    move=0 & x1<xmax & (!robot1BetweenShelves | robot1OpenRow) -> (x1'=x1+1) & (move'=1);

  • [e1] is the label of the action.
  • move=0 & x1<xmax & (!robot1BetweenShelves | robot1OpenRow) is called the guard of the action, describing whether this action is enabled or not.
  • (x1'=x1+1) & (move'=1); finishes the command by describing the outcome distribution when taking this action.

The robots may move in four directions along the axis, given they current position.

To synthesize a PreSafety-shield we define the shielding specification below. The resulting shield file will be called presafetyk14.shield as defined in the first angle brackets. We then use the keyword PreSafety along with a relative comparison of 0.9 for the shield creation. The coalition which should be shielded consists of the first player and we ask TEMPEST for the allowed actions when assuming to stay safe for the next fourteen time steps. 

<presafetyk14, PreSafety, lambda=0.9>  <<shieldedRobot>> Pmax=? [ G<=14 !"crash" ];
Figure 3: TEMPEST property specification for the safety shield. [raw]

Results

The results for the synthesis times are depicted in Figure 4. The sizes of state space of the game graphs range from 5184 states for n=2 to 186624 states for n=20. The results for optimal-shields use the axis on the right hand-side. To compare our results, we tried to compute a strategy for the optimal controller in PRISM-games 3.0 which resulted in an error. By proper modelling, we were able to synthesize a safe controller comparable to the safety-shield using PRISM-games 3.0, resulting in better synthesis times for TEMPEST.

The plot containing different synthesis times in the robotics setting.
Figure 4: The results of all three experiments for the warehouse setting. Consider the blue and green plots.